Conferencia en la Universidad de Sevilla: La historia matemática de la química

Los monos mecanógrafos contra la evolución

La extrapolación de conceptos matemáticos (o físicos) a la biología es una ocupación favorita de los grupos que niegan la evolución, eso sí, tomando algunos aspectos y desechando otros de lo que la biología tiene que decir. Una de esas extrapolaciones tiene que ver con el uso de monos mecanógrafos para demostrar que la evolución es falsa. En lo que sigue expondremos este argumento y veremos que los que lo emplean pasan por alto que los monos usan en realidad procesadores de texto, a nivel avanzado además.

Continúa leyendo en el Cuaderno de Cultura Científica

El comunismo libertario de los pingüinos.

Los comportamientos espaciales de grupos grandes de animales pueden modelarse de forma matemática habitualmente siguiendo unas reglas de comportamiento individual muy simples, aunque las matemáticas implicadas sean muy complejas. Esas reglas suelen implicar unas normas de interacción locales para el individuo que después se traducen en lo que parece un movimiento ordenado de la manada, bandada o banco. El egoísmo, la propia supervivencia, está en la raíz misma de esas normas individuales. Un nuevo ejemplo nos lo dan Aaron Waters, de la Universidad de California en Merced (EE.UU.), y sus colaboradores en un artículo que publican en PloS ONE sobre los corros de pingüinos que se forman durante las ventiscas antárticas. Una vez más, el comportamiento egoísta del pingüino individual redunda en el bien del grupo, que comparte el calor del conjunto de manera equitativa.

El funcionamiento del modelo es relativamente simple:

• Los corros son tan compactos que sólo los pingüinos exteriores pueden moverse
• Cada pingüino es una fuente de calor y el viento se lleva ese calor.
• En función del número de pingüinos en el corro y la fuerza y turbulencia del viento, el modelo calcula cuál es el pingüino más frío en el perímetro del corro.
• El pingüino más frío se mueve al lugar exterior más protegido del viento, lo que se traduce en un movimiento desde una posición cara al viento a otra resguardada de él.
• Con cada movimiento de pingüino se itera el proceso

Las iteraciones repetidas muestran que el corro se va alargando y moviéndose poco a poco a favor del viento.

Sin embargo, los corros que se ven de pingüinos no son tan alargados como señala este modelo, de hecho, tienden más a la circunferencia si no hay obstáculos como montañas cerca. Por otra parte, el modelo asume vientos constantes en velocidad y dirección y pingüinos perfectamente idénticos. Cuando los investigadores introdujeron estas variables en forma de incertidumbre, esto es, remolinos de viento y diferencias de tamaño y tolerancia al frío de los pingüinos dentro de un rango natural, el modelo pasó a reproducir muy bien las observaciones.

Una de las conclusiones del modelo es muy llamativa. Cuando los científicos calcularon cómo se repartían el calor los pingüinos se encontraron con que lo compartían casi igualitariamente. Es decir, a pesar de que el comportamiento de los pingüinos individuales es sólo egoísta, tratando exclusivamente de encontrar el mejor lugar para ellos mismos, el tiempo que cada pingüino pasa expuesto al viento es prácticamente igual. Usando un símil político-económico, del laissez-faire (dejad hacer) de d'Argenson que popularizó de Gournay nace el Jeder nach seinen Fähigkeiten, jedem nach seinen Bedürfnissen! (de cada uno según sus capacidades, a cada uno según sus necesidades) de Blanc que popularizó Marx.

Pero cuidado aquí con las extrapolaciones demasiado rápidas. No en todos los casos el comportamiento individual egoísta resulta en reparto justo. Un corro de pingüinos es un sistema autosuficiente en el que los componentes individuales dependen sólo del grupo como fuente de refugio. Las perturbaciones sencillas del sistema, como la existencia de un obstáculo (una roca grande, una montaña) al que no todos tienen acceso, rompe la equidad del reparto.

Este resultado, aparte de los beneficios que puedan extraer los biólogos especializados en pingüinos, también puede resultar interesante en el estudio de colonias bacterianas en presencia de toxinas. O, ya puestos, para diseñar pautas de comportamiento de los enjambres de robots en condiciones climáticas adversas.

Esta entrada es una participación de Experientia docet en la Edición 3,14159265 del Carnaval de Matemáticas que organiza Pi medios

Referencia:

Waters A, Blanchette F, & Kim AD (2012). Modeling huddling penguins. PloS one, 7 (11) PMID: 23166841

La geometría del hombre gordo.

Robert se sobresaltó con el timbre del teléfono a pesar de llevar esperando casi media hora desde que solicitase la conferencia.

• Profesor, el profesor...eerr...Johnny, al habla

Robert pasó por alto la falta de protocolo de su secretaria. Nadie se sentía a gusto con el apellido de Johnny.

• Johnny, aquí Robert...Sí,sí, todos bien. John, deja lo que estés haciendo y vente para aquí. Te necesitamos....Sí...Sí...Si no fuese urgente y de extrema importancia no te lo pediría de esta manera....Eso no puedo prometértelo...Sabes que no puedo darte más información por teléfono...De acuerdo, será solo una consulta para resolver este problema concreto. Estate tranquilo, sé como trabajas. Tendrás lo que necesites....Sí, ¡ja, ja! Tendrás un documento con el problema planteado y todos los condicionantes esperándote....Bien, sí, ¡ja,ja! Te veo dentro de tres días...Ah, y Johnny, ¡köszönöm!

El buen humor de la conversación se disipó pronto. Robert estaba en un callejón sin salida y recurrir a Johnny era su as en la manga. Su único as. Si Johnny no encontraba una solución, y pronto, todo el trabajo que estaban haciendo sería un auténtico desperdicio de talento, dinero y tiempo. Sobre todo de precioso tiempo.

Sabía que Johnny estaba al tanto del Proyecto en líneas muy generales, pero no de los últimos desarrollos ni de los condicionantes no puramente técnicos, así que se dispuso a prepararle un pequeño informe, suficientemente exhaustivo, para que se ubicase rápidamente tanto él dentro del Proyecto, como el problema en el contexto del desarrollo.

Informe de situación

ALTO SECRETO

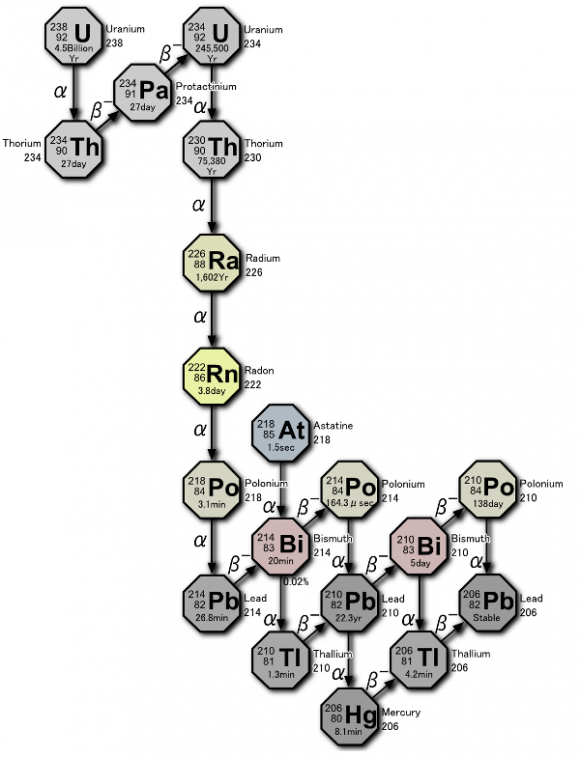
Nos falta uranio apropiado 

Tenemos localizados cuatro depósitos importantes de mineral de uranio: Colorado, norte de Canadá, Joachimstahl y el Congo Belga. Todos menos Joachimstahl están en manos aliadas. Un estudio que realizamos en 1942 afirmaba que había suficientes cantidades de uranio para satisfacer las necesidades del proyecto. Pero esto no es así por motivos técnicos. Paso a ponerte en antecedentes. 

A comienzos del siglo pasado el mineral de uranio se recuperaba como subproducto en minas de Sajonia, Bohemia y Cornualles. La primera extracción específica de menas radioactivas tuvo lugar en Jáchymov, que los nazis llaman por su nombre alemán, Joachimthal, un lugar conocido por su minería de la plata. Curie usó pecblenda de Jáchymov para aislar el radio que, como ahora sabemos, es un producto de la desintegración del uranio. 

La extracción se produce en estos lugares por el contenido en radio. Como seguramente sabes el radio contenido en las menas de uranio se usa para hacer pintura luminosa para los diales de los relojes y otros instrumentos. El uranio es un subproducto que se viene usando como pigmento amarillo. 

En los Estados Unidos la primera mena de radio/uranio fue descubierta en 1871 en una mina de oro cerca de Central City, en Colorado. Sin embargo la mayor parte se produce en la meseta del Colorado, entre Utah y Colorado, asociada a la extracción de vanadio. Aquí compramos oficialmente vanadio, pero pedimos que no lo purifiquen. Nosotros separamos después el mineral de uranio. No es un sistema muy rentable. Las concentraciones de uranio son bajas. 

Otra fuente de suministro es Port Radium, cerca del lago Gran Oso, en Canadá, donde Eldorado Mining and Refining Limited tiene grandes cantidades de residuos como consecuencia de su extracción de radio. 

Estos minerales de uranio se encuentran en rocas sedimentarias, por lo que no tienen mucho rendimiento para nosotros. 

Desde el punto de vista del rendimiento es mucho más interesante un depósito precámbrico que hay en Katanga, en el Congo Belga, descubierto en 1913, que explota la Union Minière du Haut Katanga. Nuestros amigos ingleses nos han tenido que echar una mano para conseguir que reabrieran la mina, que estaba inundada, y comenzasen a suministrarnos. 

Pero si obtener uranio nos está costando trabajo, obtener el que nos interesa mucho más. El uranio consiste en un 99,3% de uranio-238 y un 0,7% de uranio-235, pero sólo este es fisible. Ambos isótopos son químicamente idénticos y tenemos que separar el U-235 del U-238. En Oak Ridge y aquí nos hemos devanado los sesos ideando métodos de separación. 

El método más obvio, la centrifugadora, falló desde el primer momento. Ahora estamos usando separación electromagnética, difusión gaseosa y difusión térmica. A Groves se le ocurrió la idea de que el producto de una planta fuese la materia prima de otra, por lo que te puedes hacer una idea de la productividad. Tras todos estos años y esfuerzos no tenemos ni 50 kg. Con estas limitaciones no podemos ni plantearnos hacer pruebas.

La alternativa

Nos planteamos entonces aprovechar la disponibilidad de U-238 para obtener plutonio-239 que también es fisible. En un reactor nuclear bombardeamos uranio natural con neutrones. El U-238 se transmuta en U-239, que se desintegra rápidamente, primero en Np-239 y después a Pu-239. De supervisar todo esto se están encargando Fermi y Compton en un juguetito que se han construido en Oak Ridge al que llaman reactor de grafito X-10.

El problema es que sólo se transforma una pequeña cantidad de U-238, por lo que tenemos que separar el Pu-239 químicamente del uranio que no ha reaccionado, de las impurezas iniciales y de otros productos de fisión. De esto se han encargado Seaborg y Thomson con un proceso que llaman del fosfato de bismuto (otro dolor de cabeza que no viene al caso que te cuente ahora). Lo que hacen es jugar con los estados de oxidación del plutonio +4 y +6 en disoluciones de fosfato de bismuto. En las condiciones en las que el estado es +4 el plutonio precipita; en las que es +6 se queda en disolución y todo lo demás precipita. Ya te haces una composición de lugar.

Todo este trabajo con el plutonio se basaba en las propiedades que habíamos estudiado con plutonio-239 fabricado en un ciclotrón. Este Pu-239 era extremadamente puro y sólo lo pudimos crear en cantidades muy pequeñas. Cuando recibimos el primer envío desde Oak Ridge Segrè se dio cuenta de que allí había más Pu-240 del deseable, con lo que teníamos un 500% más de riesgo de fisión espontánea que con el Pu-239 puro del ciclotrón. Cuando se lo comento a Seaborg, va y me recuerda un informe que hizo hace más de un año en el que predecía que el Pu-239 puede absorber un neutrón y convertirse en Pu-240. Que él, desde el punto de vista químico, se lava las manos: si separar U-235 del U-238 era dificilísimo, separar Pu-239 del Pu-240 es prácticamente imposible.

En el dispositivo que tenemos diseñado para el U-235, que es una especie de tubo de cañón, tenemos separadas masas de material fisible que en el momento de activación son empujadas la una contra la otra por explosivos convencionales. Pero esto no lo podemos hacer con el plutonio, porque en cada trozo se podría perder suficiente energía como para dispersar la masa crítica con sólo que se desintegrase un poco de plutonio.

El problema

Necesitábamos un diseño alternativo. Neddermeyer propuso el de la implosión que, después de estudiarlo concienzudamente, nos parece viable y, a decir verdad, nuestra única esperanza de ser capaces de producir más de un dispositivo. En este método usamos explosivos para compactar una estructura subcrítica de material fisible en una forma más pequeña y densa. Cuando los átomos fisibles están empaquetados más densamente el ratio de captura neutrónica aumenta y la masa pasa a ser masa crítica. Como, en el caso que nos plantemos, el Pu-239 tiene que desplazarse un trayecto muy corto dentro del dispositivo y se mantiene a baja densidad, disminuimos la probabilidad de que se produzcan las pérdidas fatales que origina el otro método.

Las investigaciones de Neddermeyer apuntan a que vamos en la buena dirección. Pero las dificultades teóricas e ingenieriles son mucho más complejas de lo que anticipamos. Estamos colapsados. Adjuntos encontrarás los informes de Neddermeyer y los datos que puedas necesitar.

Post scriptum:

Prefiero ponerte aquí por su importancia una pequeña nota sobre normas que sí debes memorizar y cumplir a rajatabla. Las otras te las adjunto y son las habituales de seguridad en instalaciones militares de alto secreto que ya conoces.

Higiene en las instalaciones

Debes evitar todo contacto con el material fisible o sus contenedores. Debes usar bata, guantes y mascarilla si entras en el laboratorio. Se ha detectado en trabajadoras de empresas de relojería que pintan con radio muchos casos de cáncer. Muller publicó en 1927 que la radiación produce mutaciones genéticas. Además puede quemar la piel con facilidad. Las dosis altas de radiación son incompatibles con la vida.

• Estás seguro, Robert, ¿un matemático?
• Seguro, Groves. Si Johnny no lo resuelve, no lo resuelve nadie.

Hacía sólo dos horas de esa conversación y Robert la rememoraba, nervioso, mientras esperaba en la estación. Nunca antes había dependido tanto su carrera de otra persona.

Johnny bajó del tren con su traje de tres piezas impecable más propio para uno de los típicos tés de Princeton, a pesar de venir al desierto de Nuevo México. Tras los saludos habituales fueron directamente al grano. Johnny leyó el informe en el coche y ojeó los documentos adjuntos durante media hora. Después se quedó mirando el paisaje en silencio. Silencio que Robert respetaba; sabía que Johnny estaba pensando. Cuando ya divisaban las cercas del complejo Johnny habló:

• Necesitaré un sitio tranquilo en el que trabajar. Donde nada ni nadie me moleste. Y necesitaré a las dos mejores computadoras, y por mejores entiendo que hagan sus cálculos bien a la primera, con rapidez y pulcritud.
• Del lugar no te preocupes. Te he reservado un pequeño bungalow en el extremo de la base donde no te molestará nadie, yo me encargo de eso. Respecto a las computadoras le pediré a Feynman que las seleccione.
• ¿El chico de Bethe? Bien.
• Oye, Johnny, ¿por qué dos?
• Porque existe la posibilidad de que genere ecuaciones al doble de velocidad de lo que una computadora competente pueda calcular. Y no pienso pasar mi tiempo aquí esperando a que alguien termine de sumar.
• Ya veo. ¿Cuando quieres empezar?
• Ya he empezado. Estoy convencido de que el problema es básicamente geométrico.

La noticia de que Johnny estaba en las instalaciones corrió como la pólvora. Robert tuvo que dar órdenes estrictas para que nadie se acercarse a saludarle, por muy amigo, compatriota o colega que fuese.

La luz en el bungalow de Johnny no se apagó esa primera noche hasta bien entrada la madrugada. Había mandado recado de que no necesitaría a las computadoras hasta las 7 de la mañana. A las 12 del día siguiente pidieron unos sándwiches de la cantina. A las 9 de la noche las computadoras, visiblemente agotadas, regresaron a sus habitaciones del pabellón de mujeres. Johnny seguía despierto a las 2 de la madrugada. Los guardas lo veían pasear arriba y abajo en el saloncito del bungalow estudiando lo que parecían ser los mismos papeles una y otra vez.

• Profesor, eeer...Johnny está aquí.
• Gracias, Anne. Pasa, pasa, Johnny. ¿Necesitas alguna cosa? Siéntate.
• Sí, un coche que me lleve a la estación. Tal y como te dije es un problema puramente geométrico. Aquí tienes el resultado.
• Pero...
• Está más que comprobado. Funcionará. Sólo tienes que encontrar los explosivos de velocidades adecuadas. Kistiakowski es mejor que yo en eso. Dale este papel, él sabrá lo que tiene que hacer. Aquí tienes los cálculos y aquí mis conclusiones. Tu tubo de cañón se ha convertido en un hombre gordo, me temo. Léelas que me voy a casa, no aguanto el desierto.

El documento no podía ser más breve.

Conclusiones

No sólo estoy de acuerdo con que la implosión reduce el riesgo de predetonación, sino que además considero que hará un mejor uso del material fisible disponible.

Muchos de los problemas que Neddermeyer se ha encontrado surgen de usar una configuración cilíndrica. En documentos adjuntos encontrarás la demostración de que la geometría esférica es la óptima.

Recomiendo el uso de lentes explosivas para configurar una onda de choque implosiva que garantice una geometría esférica. Estas lentes explosivas están constituidas por explosivos de distinta velocidad, rápidos y lentos, cuya onda expansiva se combina hacia dentro para obtener la geometría buscada. Los parámetros a buscar experimentalmente están dentro de los rangos que te especifico en el documento adjunto.

Es muy probable que la configuración óptima, dependiendo de los explosivos disponibles y sus características, esté constituida por 20 hexágonos y 12 pentágonos alrededor del núcleo esférico de material fisible, según este esquema:

                                           

• ¿Están claras?
• Diáfanas.
• Pues me voy. ¿Está el coche?
• No vas a ver a los muchachos. Están deseando saludarte.
• No, son demasiados. Ya he charlado un rato esta mañana con Ulam y Feynman y ya es suficiente para mí. Hasta nos han hecho una foto. Sólo diles que von Neumann estuvo aquí. Ellos entenderán.

                                                                       

Pasados los años Robert conservaba una copia de aquella foto. Representaba para él el momento cumbre del proyecto antes de la prueba, cuando supo que lo lograrían: en la foto aparecían sus muchachos agotados después de meses dando lo mejor de sí mismos y un genio venido de otro mundo que solucionaba con matemáticas lo que aquellos físicos y químicos brillantes metidos a ingenieros no alcanzaban.

Esta entrada es la modesta respuesta de Experientia docet al reto de redactar un texto con la capacidad de participar en 7 carnavales (matemáticas, física, química, biología, geología, tecnología y humanidades).

A efectos prácticos esta entrada es una participación de Experientia docet en la XVIII Edición del Carnaval de Química (en XdCiencia), en la XXXV Edición del Carnaval de la Física (en Últimas noticias del cosmos) y en la 3,1415926 del Carnaval de Matemáticas (en Series divergentes).

Una aproximación a la leyenda del mecanismo de Higgs (relato fragmentario)

En el comienzo sólo existía una, unificada y todopoderosa fuerza llamada la Superfuerza para gobernar el Universo. Pero una fracción minúscula de segundo después de que el universo comenzase a ser, la Superfuerza comenzó a descomponerse, proveyendo sucesivamente para la Gravedad que actúa en todo el Universo y la Forzuda (la lamada Carcelera, la que mantiene atrapados a los Quarks dentro de las prisiones Protón y Neutrón). 

Tras parir a Gravedad y Carcelera, la Superfuerza quedó reducida a tres hermanos mellizos: Electricidad, Magnetismo, y Debilucha (una radioactivista que establecería la vía de escape de las macroprisiones Núcleo conocida como desintegración beta). Los tres hermanos eran en esta época como si fuesen uno y sus sirvientes llamados Fotón, W+, W- y Z, vivían con ellos en paz y armonía. Los sirvientes se parecía mucho entre sí y se comportaban igual.

Los Mellizos dentro de Superfuerza. Debilucha de pie. Nótese la mirada libidinosa de Electricidad a Magnetismo.

Pero no seguirían así mucho tiempo. Un campo misterioso permeaba el Universo. Un campo extraño que, como Magnetismo o Gravedad, podía rodear a un objeto pero que, a diferencia de ellos no asociaba una dirección. No apuntaba a ninguna parte, simplemente estaba. A diferencia de los hijos de la Superfuerza, los orgullosos y omnipotentes Vectoriales, ese campo era un humilde Escalar. Su nombre revelaba su baja extracción: Campo de Higgs.

El Campo de Higgs tenía problemas psiquiátricos. Los especialistas dirían después que tenía rasgos esquizoides y paranoides o, según otros, doble personalidad compleja. Esto quería decir que tenía aspectos de sí mismo que eran imaginarios entrecruzados con otros que eran reales. La cuestión es que familiares y amigos para poder entenderlo y relacionarse con él lo trataban como si fuese cuatro (en la escuela, los campiños, crueles, le cantaban “Higgs tiene cuatro dimensiones, Higgs tiene cuatro dimensiones”) y hacían la vista gorda porque tuviese un sirviente capaz de satisfacer sus cuatro facetas, un sirviente cuatridimensional, que en realidad eran cuatro.

Y entonces ocurrió. La Gran Guerra que cambió el Universo. El Campo de Higgs interactuó con los Mellizos.

Fue una guerra noble, en la que los señores mandaron a sus sirvientes a luchar. Debilucha, cuyo nombre es harto engañoso, hizo gala de las habilidades que después la harían famosa y dirigió a sus tres sirvientes (W+, W- y Z) en el combate con tal destreza que cada uno de ellos salió triunfante de su colisión con un sirviente del Campo de Higgs, enguyéndolo. Por esta victoria les fue concedido el más alto honor, tomar botín, la masa.

Sin embargo Electricidad y Magnetismo, centrados en lo que después se supo que era un amor incestuoso, fracasaron miserablemente. Como resultado de la Gran Guerra W+, W- y Z consiguieron masa, Fotón huyó cobardemente a la máxima velocidad permitida y quedó libre, aunque oculto y huidizo, el cuarto sirviente del Campo de Higgs.

Algunos trovadores comenzaron a contar la leyenda del “mecanismo de Higgs”, ya se sabe el atractivo que para algunos tienen los perdedores. Según ella el Campo de Higgs dio masa a los sirvientes, que dijeron pertenecer a la tribu de los Bosones, los portadores de fuerza, W+, W- y Z y no sólo a éstos, sino a los Quarks y a los Electrones. La leyenda también afirmaba que el sirviente de Higgs era un bosón. A partir de aquí ya los libros de historia ortodoxos coinciden más.

Cuando el Universo comenzó a enfriarse ligeramente, los Quarks vivían en una comuna gigantesca, la famosa Sopa de Quarks, pero con el tiempo y el enfriamiento consiguiente, Forzuda, acusándolos de colaboracionistas empezó a encerrarlos de tres en tres en las prisiones Neutrón y Protón. La eficiencia administrativa llevó a la creación de asociaciones carcelarias llamadas Hidrógeno, Helio y Litio. Gravedad entró a colaborar y empezó a unir esas primeras asociaciones en centros de concentración llamados Estrellas. Las agrupaciones territoriales de Estrellas fueron llamadas Galaxias.

Las condiciones de hacinamiento en las cárceles estelares llevaron a fusiones y adquisiciones de las asociaciones carcelarias menores, creando nuevas más grandes y complejas: Carbono, Oxígeno, Hierro. En esta época comenzaron a producirse motines en algunas estrellas. Se volvieron tan comunes que hasta recibieron un nombre, Supernovas. Aún así los Quarks huían de sus prisiones gravitatorias, pero no de las forzudas. Y eso que Debilucha permitía ya escapar a algunos rebeldes vía desintegración beta.

La leyenda no cuenta en qué batallas los Electrones o los Quarks ganaron su masa. Sí sabemos que los sirvientes del Campo de Higgs, aislados y huidizos, eran higgsófagos, peleaban y se comían entre sí, dándose masa entre ellos, deshonrándose. El Fotón cuando no hay nadie alrededor sigue huyendo a máxima velocidad, sólo cuando atraviesa materia la baja algo, como para disimular.

[El Universo mismo escribió la historia original usando Matemáticas. Los humanos estamos aprendiendo el lenguaje para intentar leer el libro completo y no tan sólo fragmentos inexactos e inconexos como éste]

Cómo usar uranio para saber si un neandertal pintó en una cueva.

En estos días ha habido mucho revuelo mediático con la posibilidad de que los neandertales hubiesen tenido la oportunidad de ser los pintores de Altamira y otras 10 cuevas del norte de España (véase este enlace como ejemploy más datos) . A lo que no se ha prestado atención alguna es al método empleado, que en el artículo publicado en Science, Pike et al. llaman “datación por serie U”. Vamos a explorar la base teórica (incluidas las matemáticas) del mismo, que es muchísimo más sencilla que la experimental, porque si bien no hay nada más práctico que una buena teoría, también es cierto que aún no debiendo haber teóricamente diferencia entre teoría y práctica, en la práctica, la hay.

Los investigadores usaron los ratios entre los isótopos uranio-234 y torio-230 para datar los depósitos de calcita sobrepuestos a las pinturas para calcular la edad mínima de las mismas. Los resultados, con edades mínimas en el entorno de los 40.000 años de antigüedad, abren distintas posibilidades. Como se supone que Homo sapiens sapiens no migró a Europa hasta hace poco más de 40.000 años es probable que trajese sus habilidades artísticas africanas con él y decorase las cuevas poco después de llegar o, quizás, las pinturas más sencillas y antiguas fuesen de hecho la obra de neandertales.

La datación uranio-torio es especialmente interesante en el análisis de carbonatos cálcicos, como la calcita, ya que ninguno de los elementos puede escapar del mineral, ni otros átomos de ellos pueden entrar, una vez se ha formado. En las condiciones de formación de las calcitas el uranio es soluble mientras que el torio no lo es, por lo que cuando se forma el depósito mineral contendrá uranio pero no torio. La cantidad del isótopo U-234, que es el isótopo que por desintegración alfa se convierte en torio 230, que podemos esperar tener en una calcita recién formada es del orden de partes por millón o inferiores. Suponiendo que sepamos la cantidad original de uranio presente en la muestra, necesitamos poder calcular cuánto Th-230 tendremos pasado un tiempo a partir de una determinada cantidad de U-234 para tener un método para determinar el tiempo transcurrido.

Imaginemos que el isótopo A se desintegra para dar B, por el proceso que sea: A → B. La desintegración de un núcleo inestable es algo completamente aleatorio y es imposible predecir cuándo un átomo en concreto se va a desintegrar. Sin embargo, la probabilidad es igual en cualquier tiempo t. Si tenemos un número N de núcleos de un isótopo concreto, transcurrido un tiempo infinitesimal, que llamaremos dt, se habrán desintegrado un número infinitesimal de núcleos, dN, quedando N-dN. Por otra parte, el número de desintegraciones que se produce en la unidad de tiempo, -dN/dt, debe ser proporcional al número de nucleones presente, igual que en una sala en silencio el número de toses es proporcional al número de personas presentes, como bien saben los músicos de clásica. Así, si llamamos a la constante de proporcionalidad característica de ese isótopo λ, podemos escribir:

-dN/dt = λN

Esto es una ecuación diferencial muy sencillita que el lector puede comprobar que tiene como solución

N = N₀ e^-λt , donde N₀ es el número de átomos pata t = 0. [1]

Sin embargo, el sistema U-234 - Th-230 no es tan sencillo, puesto que el Th-230 también se desintegra. Estamos entonces ante esta situación: A → B → C. El razonamiento es análogo: si tengo N núcleos, pasado un tiempo infinitesimal dt, tendré N+dN núcleos. En este caso escribo +dN, porque dN puede ser positivo o negativo, dependiendo de si se forman más núcleos de los que se desintegran o al revés. En cualquier caso, la variación en el número de núcleos será los que se forman menos lo que se desintegran, por tanto, usando [1]:

dN_B/dt = λ_AN_A – λ_BN_B = λ_A N_0A e ^-λAt – λ_BN_B

Esto sigue siendo una ecuación diferencial nada complicada, que se puede comprobar que tiene como solución:

N_B = (N_A0 λ_A) / (λ_B - λ_A) · (e ^-λAt - e ^-λBt) [2]

En pura teoría ya tenemos la ecuación que buscábamos. Si conocemos las constantes de los isótopos U-234 (que ocupa el lugar de A) y del Th-230 (B), que las conocemos, tendríamos un método para medir la antigüedad de los depósitos de calcita.

El inteligente lector que haya llegado hasta aquí se habrá dado cuenta de que venimos arrastrando un problema no menor desde el principio: ¿cómo sabemos qué cantidad había al comienzo del isótopo A, lo que hemos llamado N_A0? Simplemente, no lo sabemos, ni lo podemos saber con suficiente precisión. Por eso un método de datación que se base en una serie radioactiva sólo es válido si uno de los núcleos es estable (λ_B = 0) o, como el caso de U-234 y Th-230, que se cumpla que

0 < λ_A << λ_B

Entonces [2] queda reducida a

N_B / N_A ≈ λ_A / λ_B (1 - e ^-λBt) [3]

Ya que también en este caso, N_A ≈ N_A0.

Vemos pues que si medimos por espectrometría de masas el ratio Th-230/U-234 tenemos una forma directa de medir el tiempo desde que se formó la calcita con un error más que razonable. Sólo nos quedará corregir por la cantidad de U-238 que se convierta en U-234, pero eso es más de lo mismo (se deja al lector como ejercicio).

Observando la ecuación [3] vemos una de las limitaciones del método: para tiempos suficientemente grandes N_B / N_A tiende a un valor constante λ_A / λ_B, es lo que se denomina equilibrio secular (se forma tanto Th-230 como se destruye). Por tanto el método uranio-torio no puede datar más allá de 500.000 años, aproximadamente.

Esta entrada se publica conjuntamente en Amazings.es y es una participación en la Edición 3,14159  del Carnaval de Matemáticas que organiza Scientia y en la XVI Edición del Carnaval de Química  que alberga ¡Jindetrés, sal! 

Referencia:

Pike AW, Hoffmann DL, García-Diez M, Pettitt PB, Alcolea J, De Balbín R, González-Sainz C, de las Heras C, Lasheras JA, Montes R, & Zilhão J (2012). U-series dating of Paleolithic art in 11 caves in Spain. Science (New York, N.Y.), 336 (6087), 1409-13 PMID: 22700921

La leyenda de Helgoland

Yo soy Forseti, el más sabio y elocuente de los Æsir.

Yo soy Forseti, el hijo de Baldr y Nanna.

Yo soy Forseti, la paz de Asgard, hogar de Odín y Frigg.

Yo soy Forseti, el que dirime disputas y es adorado en Forsetalundr.

Yo soy Forseti, el que reside en Glitnir, la del techo de plata y columnas de oro.

Glitnir heitir salr,

hann er gulli studdr

ok silfri þakðr it sama;

en þar Forseti

byggvir flestan dag

ok svæfir allar sakar.

Oye la voz de Forseti, porque él busca la justicia. Escucha, ¡oh mortal!, lo que ha de suceder. Esta es la voluntad del Señor de Hliðskjalf. Tras la Gran Guerra, un hombre del sur llegará al lugar que es verde, rojo y blanco buscando respirar. Pero son las disputas con el jefe vikingo y su lugarteniente las que asfixian su alma. Él es mi elegido. Deberá olvidar lo que ya sabe y aprender lo que ya sabe para darse cuenta de que es diferente. Y de esta forma los mortales verán, pero será borroso; entenderán, pero no comprenderán.

Deät lun, la tierra, así la llaman sus habitantes en halunder. No necesitan más. Pero los germanos del sur la conocen como Heyligeland, la tierra sagrada, porque es la tierra elegida por Forseti, el que preside, der Vorsitzender. Es la isla de Helgoland. Y esta es su leyenda.

El barco rodeó la pequeña isla buscando la ensenada. Por esa parte aparecía ante los escasos viajeros como una pared vertical rojiza. Sin embargo, al alcanzar la ensenada una playa blanquísima daba paso a la dársena. El pueblo empezaba en la misma playa y escalaba la pendiente suavizada del acantilado hasta llegar a la verde planicie superior.

En el pequeño puerto aún podían verse restos de la base que había sido destruida en la primera batalla naval de la Gran Guerra. Pero el viajero no estaba demasiado interesado en la historia. Desde que había zarpado del continente había comenzado a sentirse mejor y ya casi podía decirse que respiraba con normalidad. Mientras el barco iniciaba las maniobras de atraque, observaba con satisfacción que en la estrecha isla no había ni un sólo árbol, ni siquiera un arbusto que levantase más de una cuarta del suelo. Aquel era el lugar ideal para pasar una temporada dedicado a recuperarse de su alergia, leer a Goethe e intentar resolver algunos problemas que con Bohr y sus filosofías cerca eran difíciles de afrontar con tranquilidad. Era el 8 de junio de 1925.

Para el joven Heisenberg la naturaleza era su refugio. En el aislamiento de Helgoland podría dedicarse a pasear, a descansar, a pensar. Efectivamente, a los pocos días su salud estaba reestablecida, los vientos del mar del Norte estaban limpios y abrían sus pulmones. Sus paseos comenzaron a ser más enérgicos y, sin prácticamente nadie con quien hablar, la niebla que había en su mente también empezó a aclararse.

Tras terminar su estancia en Copenhague con Bohr, y el insufrible Kramers, ya de vuelta en su universidad, Heisenberg no había tenido ninguna dificultad en escribir, formalmente desde un punto de vista matemático, unas ecuaciones que expresaban la posición y la velocidad de un electrón como la combinación de las oscilaciones fundamentales de un átomo. Pero cuando insertaba estas expresiones compuestas en las ecuaciones estándar de la mecánica el resultado se parecía mucho al caos absoluto.

Donde debería haber un número aparecían listas de ellos, el álgebra no podía ser más elemental y, sin embargo, explotaba llenando páginas y páginas de fórmulas repetitivas. Durante semanas Heisenberg había intentado diferentes cálculos, jugando con el álgebra desde todos los ángulos que se le ocurrían. Recurrió a su salvavidas habitual, las series de Fourier, pero sin éxito.

Fue en ese punto cuando el aire de Gotinga pareció convertirse en una sopa irrespirable y Max Born le recomendó la isla como alivio para su ataque de asma alérgico.

Durante sus paseos por Helgoland llegó a un primer diagnóstico del problema que después se revelaría fundamental: la dificultad estaba en la multiplicación. Había convertido posición y velocidad de números sencillos a sumas de varios términos. Multiplicar dos números entre sí produce otro número. Multiplicar dos listas de números produce una página entera con todos los términos posibles resultantes de las distintas combinaciones: cada número de la primera multiplicado por todos los de la segunda. Pero ¿qué términos eran importantes? Y ¿cómo deberían sumarse para que el resultado tuviese algún sentido? Aquello era un rompecabezas sin sentido.

Ocurrió entonces, que una noche, cuando se disponía a cenar en el pequeño hostal en el que se alojaba, se encontró con otro huésped, algo extraño en aquel lugar. No fue difícil entablar conversación, no había nadie más en aquella habitación y, después de tanta soledad, resultaba un alivio poder charlar intrascendentemente con alguien. El viajero, que dijo llamarse Gangleri, de una edad indefinida y luciendo una larga barba, afirmaba dedicarse a vagar por el mundo descubriendo sus maravillas. Era magnético, con una curiosidad e inteligencia siempre alertas. Antes de que se diese cuenta, Heisenberg le estaba contando en términos sencillos a qué se dedicaba y cuál era su problema.

Gangleri escuchaba con atención con un brillo en los ojos. Cuando el joven físico terminó de hablar, sonrió y, bajando el tono de voz tanto que apenas susurraba, dijo: “Deja de pensar como un hombre. Piensa como lo harían los dioses, para los que el orden es de la máxima importancia”. Tras mirar fijamente a los ojos a Heisenberg y sonreír enigmáticamente, se levantó y dio las buenas noches. Nadie volvió a verlo.

Heisenberg se quedó un rato más fumando. No podía dejar de sonreír pensando en lo que Ganglieri había dicho y, no porque le diese la menor importancia, sino porque le recordaba a la mezcla de física y misticismo que en el Instituto de Copenhague le habían contado que era tan del gusto de Einstein.

Una cosa llevó a otra y en la mesa del comedor Heisenberg sacó sus papeles para dar un poco de forma a sus pensamientos del día. Había intentado olvidarse de las matemáticas y concentrarse en la física. Los elementos de su álgebra eran oscilaciones, cada una representando una transición de un estado a otro. El producto de dos de estos elementos debería representar una doble transición, de un estado a un segundo y de éste a un tercero. Entonces le pareció escuchar la voz de Gangleri: el orden. Reflexionó: la forma de ordenar esta tabla de multiplicaciones era poner juntos los elementos que correspondían al mismo estado inicial y final, sumando todos los intermedios posibles. De esta manera tenía una regla de multiplicación que era a la vez manejable y con sentido. Y, satisfecho, se fue a la cama.

Pero no pudo dormir. A las tres de la mañana ocurrió. Lo que había garabateado sin pensar demasiado en la mesa del comedor podía ser más importante de lo que había creído. ¿Y si los cálculos demostraban que había dado en el clavo? Incapaz de conciliar el sueño saltó de la cama y se puso a trabajar en un estado de gran excitación. Era tal su nerviosismo que cometió innumerables errores aritméticos elementales. Tras horas de trabajo y para su asombro y estupefacción obtuvo una respuesta: sus extrañas matemáticas daban como resultado una energía para el sistema que era consistente, pero siempre y cuando la energía tomase valores discretos, no continuos. ¡Su sistema daba una energía cuantizada sin que hubiese que introducir la cuantización entre las hipótesis de partida!

Nunca antes había ocurrido esto. La hipótesis de Planck había que introducirla “a mano” en algún momento. Pero no en su sistema. Él había escrito las ecuaciones estándar para un sistema mecánico sencillo, había insertado sus expresiones compuestas para la velocidad y la posición, aplicado su nueva regla de multiplicación y la cuantización surgía de las matemáticas. La energía de un sistema mecánico se autocuantizaba. Sin más.

Entusiasmado salió al exterior y corrió a una de las rocas de la orilla donde se tumbó a disfrutar del sol naciente, embelesado con su descubrimiento, en éxtasis.

En el camino de regreso a Gotinga sólo una cosa le preocupaba. Su método de multiplicación no era reversible. Los matemáticos dirían que no era conmutativo: a por b no daba el mismo resultado que b por a. Pero los dioses le favorecían. Gotinga era el Olimpo de las matemáticas y su jefe, Born, tenía una formación matemática de primer nivel. Cuando Heisenberg le presentó un borrador con su descubrimiento, tras la sorpresa inicial, a Born no le costó identificar que lo que estaba viendo no era más que una forma de una oscura, y casi olvidada, rama del álgebra llamada álgebra de Grassmann, en la que los elementos no eran números sino disposiciones de números llamadas matrices. Tras algunas pequeñas correcciones, Born mandó a publicar el escrito rápidamente en Zeitschrift für Physik, ya habría tiempo de refinarlo.

A los pocos días, Born informaba a Einstein del hallazgo. En la nota que le envió decía “parece muy místico, pero ciertamente es correcto y profundo”.

Había nacido la mecánica cuántica.

Notas:

1. Esta entrada es una participación en la Edición 3.1415 del Carnaval de Matemáticas que acoge Gaussianos.
2. Lo que antecede es creación mía. No existe una Leyenda de Helgoland fuera de esta entrada. Eso sí, está basada en hechos reales.
3. Ningún nombre de esta entrada está inventado ni está elegido al azar. Todos remiten a a algo cuyo hallazgo dependerá de la curiosidad del lector.
   
   
   
   
   

La estructura del azar y el i-Phone 5

Esta entrada tiene dos partes diferenciadas y autocontenidas; si te interesa el aspecto tecnológico exclusivamente puedes pasar a la segunda (Estructura a nanoescala de un vidrio metálico) sin necesidad de leer la primera, de contenido algo más matemático y especulativo.

Proyección ortográfica de un cubo de 5 dimensiones en 2 dimensiones sobrepuesto al patrón de difracción de un cuasicristal icosaédrico

Los servicios de inteligencia sabían muy bien en la época de la Segunda Guerra Mundial la importancia que la verdadera aleatoriedad tenía en los códigos que usaban sus espías para encriptar sus mensajes. Ya habían descubierto durante la Primera, de la forma más dolorosa, que una persona no puede escribir números realmente “al azar” y, por ello, en Bletchly Park, sede de los servicios de contraespionaje británicos, donde trabajó Alan Turing y se descifró el código de la máquina Enigma, había grupos de mujeres arrojando dados con los que construían cuadernos de un solo uso pseudoaleatorios para que los usasen los espías en el continente.

Construir secuencias aleatorias puede parecernos intuitivamente fácil, pero no lo es. No se trata de decir los números (letras o palabras son reducibles a números) que se nos ocurran y y ya está. Hemos de tener cuidado de que no dejemos, inconscientemente, una pauta: tendemos a usar determinadas palabras y estructuras gramaticales, por ejemplo. Pero, paradójicamente, intentar no dejar una pauta, ¡es una pauta! Estos es sólo la manifestación del hecho de que el azar, la pura aleatoriedad, contraintuitivamente, tiene estructura. Veamos un ejemplo.

Intenta escribir una secuencia de números naturales que tú creas que es aleatoria. Una vez que lo hayas hecho estudiala como si la hubiese escrito otra persona y busca pautas; las encontrarás rápidamente. Así, si nos limitamos a los números naturales entre 1 y 15 podríamos haber escrito:

1, 4, 6, 7, 10, 14

que parecen números al azar. Pero a estos números se le puede encontrar una pauta:

a, a+n₁3, b, a+n₂3, a+n₃3, 2(b+1) donde n = 1, 2, 3, ...

Dicho de otra manera, 1,4,7 y 10 forman una progresión aritmética en el que la diferencia entre un término y el siguiente es la misma (3). Sabiendo esto intentemos elegir los números de forma que no haya ningún tipo de pauta apreciable entre ellos:

1, 2, 4,

Con estos números ya no podemos elegir el 6 por que tendríamos 2, 4, 6, así que

1, 2, 4, 5,

y ahora no podemos elegir ni el 7 ni el 8...

Y esto es limitándonos a las progresiones aritméticas. Hemos podido ver que escribir una lista de números al azar no es trivial. De hecho el teorema de Szemerédi prueba que es imposible. Y rizando el rizo, ni siquiera usando números primos te libras del problema, como demuestra el teorema de Green-Tao.

Cuando consideramos los sólidos el concepto de aleatoriedad se asocia a los sólidos amorfos, a los llamados vidrios. En estos se dice que el empaquetamiento de los átomos, la secuencia en la que se colocan es aleatoria. Esto podríamos llegar a la conclusión de que no es cierto gracias a Szemerédi, aunque hay cuestiones puramente químicas que nos hacen intuir que esto no puede ser estrictamente así.

Por su estructura interna los sólidos podemos clasificarlos en cristalinos, cuasicristalinos y amorfos. Como las definiciones estándar de estas estructuras se pueden encontrar fácilmente en la red, nosotros vamos a ir un pasito más allá y hablaremos de hiperdimensiones y de los planteamientos sobre aperiodicidad de Harald Bohr para unificar matemáticamente la visión de las tres. Así, una estructura cristalina sería el corte de una función multidimensional periódica por un hiperplano racional, es decir, la estructura cristalina tridimensional es realmente el corte por un hiperplano según un plano de la celda hexadimensional. Análogamente, en un cuasicristal el corte de la función periódica es irracional (típicamente el número áureo), esto es, el hiperplano que corta no coincide ni puede hacerse coincidir con un plano de la celda hexadimensional.

Vemos que, desde este punto de vista, hemos agotado todas las posibilidades de corte de una celda hexadimensional con los cristales (números racionales) y los cuasicristales (irracionales). Por tanto, podemos conjeturar [lo que no he leído en ningun parte y es original de un servidor] que en un sólido amorfo, de existir hiperestructura, ésta tendrá una dimensionalidad superior a 6 pero finita. Y es finita por el teorema de Szemerédi y porque a corto rango existe orden en todos los sólidos.

Efectivamente, desde el punto de vista del orden tanto cristales como cuasicristales lo tienen a corto a medio y a largo. Es característico de los cuasicristales que existan simetrías icosaédricas, cosa que para los cristales no está permitida, y el orden a largo no es tan evidente. En los vidrios no existe orden a largo (en el sentido habitual del término, hay aleatoriedad), pero sí existe orden a corto porque químicamente los átomos sólo son estables o metaestables en determinados entornos. Se alcanzará un estado estable si la mezcla tiene tiempo y energía como para ordenarse suficientemente, si no, el estado será metaestable. La cuestión es ¿cómo es la transición del orden a corto al desorden a largo? ¿habrá fases cristalinas, cuasicristalinas? ¿Qué ocurre a medio rango?

Un indicio del aspecto que pueden tener las respuestas a estas cuestiones lo proporciona un grupo de investigadores encabezados por Jinwoo Hwang, de la Universidad de Wisconsin en Madison (EE.UU.), con los resultados que han publicado en Physical Review Letters sobre un vidrio metálico.

Estructura a nanoescala de un vidrio metálico.

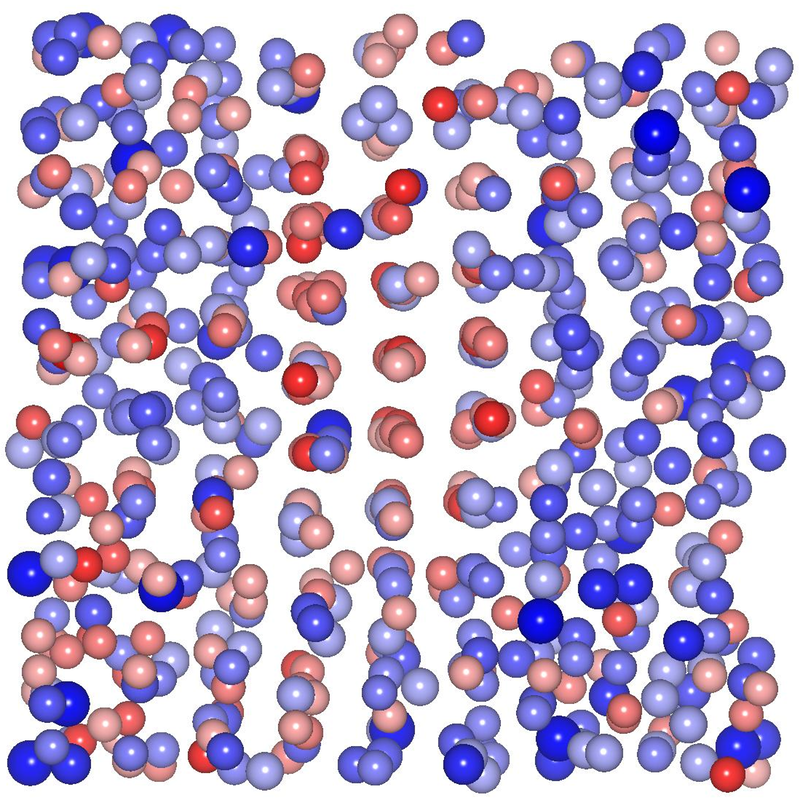Zonas de estructura cúbica (centro) e icosaédrica (bordes) en un vidrio metálico

Los vidrios metálicos (VM) tienen características técnicas muy interesantes: son metales, son fuertes, y resisten muy bien la corrosión y el desgaste. Pero pueden romperse de pronto. El conocimiento que se tiene de su estructura es muy limitado como para poder explicar estas características. El trabajo de Hwang et al., del que damos la referencia más abajo, sugiere que estos materiales contienen más orden de lo que sugiere su nombre.

Los especialistas en materiales sospechan que los VM tienen algún tipo de estructura semiordenada, aún cuando no sea un cristal perfecto. La teoría predominante, apoyada por modelos por ordenador, es que hay “agrupaciones” de átomos, entendiendo por agrupación un átomo central y sus vecinos inmediatos, que forman pentágonos distorsionados o, más bien, icosaedros, sus equivalentes tridimensionales. Estas geometrías tienen simetría traslacional quíntuple, por lo que estaríamos frente a estructuras tipo cuasicristal. Los materiales con esta estructura tienden a quebrarse bajo tensión, en vez de estirarse o doblarse, lo que coincide con los VM. Hay otra teoría que dice que hay varias agrupaciones que se organizan en disposiciones cristalinas de tamaños del orden de un nanometro, pero esto suscita más polémica.

Hwang et al. han añadido datos experimentales a un modelo por ordenador y el resultado es que la realidad sería más compleja que ninguna de estas hipótesis por separado.

El equipo de investigadores usó una técnica llamada microscopía electrónica de fluctuación (FEM, por sus siglas en inglés) para estudiar muestras de un VM de composición Zr₅₀Cu₄₅A_l5. La FEM mide las variaciones en la difracción de los electrones conforme un flujo de éstos se mueve por la superficie de una muestra delgada. Una muestra perfectamente homogénea, ya sea cristalina o amorfa, no tendría variaciones significativas en su modelo de difracción. Pero si la muestra tiene algún tipo de variación en la escala de uno a unos pocos nanometros la difracción cambiará de forma significativa. La técnica, por tanto, es sensible a lo que se denomina rango medio, el rango donde la microscopía electrónica convencional o la difracción rayos X tiene dificultades.

Los datos de la FEM se introdujeron en una simulación por ordenador (Montecarlo híbrida inversa) con el resultado de que diferentes zonas de la muestra tenían diferentes simetrías. Unas eran icosaédricas y otras eran cúbicas. Las zonas cúbicas podían llegar a ser el 15% de la muestra. Como ésta se había enfriado muy rápidamente desde su estado fundido, la estructura alcanzada es muy probable que sea metaestable.

Efectivamente, cuando la muestra se calentaba durante una hora a la temperatura de la habitación, el porcentaje de zona cristalina caía drásticamente pasando a una estructura icosaédrica. Esta estructura sería más estable, por tanto.

Decimos más estable y no la más estable porque puede que el estado alcanzado sea el de energía más baja. Esto, unido a que el estudio se refiere a un VM muy concreto, implica que no se puede generalizar el resultado a otros tipos de VM con facilidad. Pero, como todos los VM se fabrican por enfriamiento muy rápido, sí nos da indicios de lo que puede llegar a ocurrir con su uso industrial.

El iPhone 5 y los vidrios metálicos

Una de las características de los vidrios es que no tienen una temperatura de fusión, es decir, una temperatura a la que pasan del estado sólido al líquido. Por el contrario la transición de sólido a líquido es continua: los vidrios pueden visualizarse como líquidos de viscosidad muy próxima a infinita que, conforme se calientan, van disminuyendo progresivamente, empezando a fluir cada vez más. Esto los asemeja a los plásticos, que se van “derritiendo” cuando los calentamos haciéndose cada vez más maleables.

A diferencia, por tanto, de las aleaciones metálicas habituales, los vidrios metálicos pueden moldearse como el plástico: los puedes aspirar, empujar, soplar o lo que se te ocurra para que adopten formas muy complicadas sin pérdida de material y sin mecanización.

Si esto sigue siendo cierto incluso a micro o nanoescala podrías fabricar haces de nanocables o microengranajes para micromotores. El problema surge con el comportamiento a medio rango, que viene condicionado por la más que posible existencia de estructuras cristalinas metaestables, en principio, no deseadas.

Si el rumor de que el próximo iPhone 5 usará intensivamente VM es cierto, Apple estaría poniendo un montón de fe en un material cuyas características los científicos sólo están empezando a comprender.

Esta entrada es una participación de Experientia docet en la XV Edición del Carnaval de Química que organiza El cuaderno de Calpurnia Tate.

Referencia:

Hwang, J., Melgarejo, Z., Kalay, Y., Kalay, I., Kramer, M., Stone, D., & Voyles, P. (2012). Nanoscale Structure and Structural Relaxation in Zr_{50}Cu_{45}Al_{5} Bulk Metallic Glass Physical Review Letters, 108 (19) DOI: 10.1103/PhysRevLett.108.195505

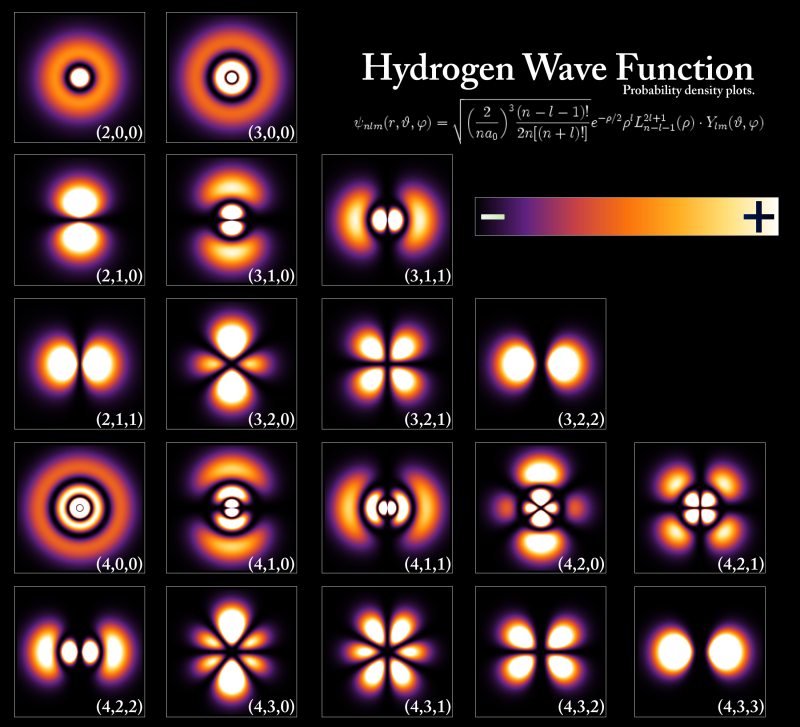
El origen matemático de los números cuánticos y de los orbitales atómicos.

En muchas ocasiones, cuando nos enfrentamos a la derivación de las expresiones matemáticas que representan sistemas físicos la mezcla precisamente de conceptos matemáticos y físicos hace que ni sigamos unos ni entendamos los otros. Nosotros pensamos que explicar ambas por separado ayuda en gran medida a la comprensión general.

Ayer, el hijo de un amigo nos planteaba que aceptaba la forma de los orbitales del átomo de hidrógeno y la aparición de los números cuánticos (salvo el de espín) como si fuesen un dogma, declarándose incapaz de seguir ni a su profesor ni a su libro de texto (el chaval estudia segundo de químicas en una prestigiosa universidad española). Es mi opinión que ello se debe a que las matemáticas y la física ya son lo suficientemente sutiles (me niego a aceptar que sean complicadas) por separado como, para encima, mezclarlas.

Lo que sigue es una explicación, un esquema conceptual si se quiere, de cómo se llega a los orbitales del átomo hidrogenoide (un átomo que tenga sólo un electrón) y a los 3 números cuánticos asociados (el de espín va aparte) desde un punto de vista matemático. Una vez que se tiene claro “cómo” lo haces ya te puedes concentrar en “qué” haces. Como conocimientos previos está saber lo que es una ecuación diferencial y cómo se resuelve en términos generales.

La llamada función de onda, que es la que describe la posición del electrón (por simplicidad excluimos la dependencia del tiempo), no es más que una función de tres variables que viene descrita por una ecuación diferencial llamada ecuación de Schrödinger (EdS) que adopta la forma

HΨ = EΨ                                [EdS]

donde H es un operador llamado hamiltoniano. Este operador a su vez lo podemos expresar de tal manera que la EdS la podemos escribir como

HΨ= aΔΨ + bΨ/r = EΨ           [EdS]

en la que a y b son constantes, Δ es el operador laplaciano y r es una distancia (la del electrón al núcleo). El operador laplaciano no es más que la suma de las derivadas parciales segundas con respecto a cada una de las tres variables, es decir:


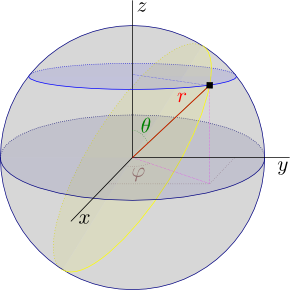
a(∂²Ψ /∂x² + ∂²Ψ /∂y² + ∂²Ψ /∂z²) + bΨ/r = EΨ [EdS]

r = (x²+y²+z²)^1/2

Coordenadas esféricas físicas.

La resolución de esta ecuación diferencial nos proporcionará Ψ, que es lo que queremos. Sin embargo esta resolución en coordenadas cartesianas se hace muy complicada y es preferible usar coordenadas esféricas. En estas coordenadas Ψ pasa de ser una función de x, y, z a ser una función de r, θ y φ donde

x = r sen θ cos φ

y = r sen θ sen φ

z = r cos θ

Haciendo la sustitución resulta que la función Ψ puede expresarse como el producto de tres funciones cada una de una sola variable, Ψ= R(r)Θ(θ)Φ(φ), con lo cual obtenemos tres ecuaciones diferenciales independientes, cada una en una sola variable. Ya sólo nos queda resolver estas ecuaciones. No vamos a entrar aquí en cómo se hace, nos limitaremos a señalar unos detalles matemáticos que después se revelarán como muy importantes.

En la resolución de Φ(φ) nos va a aparecer una constante de separación que, convencionalmente (tiene un sentido físico), llamaremos m. Para que se cumpla que Φ(φ) = Φ(φ +2π), m sólo puede ser un número entero (positivo, negativo o cero).

La resolución de Θ(θ) es más complicada. En ella aparece de nuevo m y una nueva constante de separación l. Las condiciones que deben cumplir las soluciones (que sean cuadráticamente integrables) obligan a que l = |m|, |m|+1, |m|+2,.... Esto quiere decir que el valor más pequeño de l es cero y que m va de -l a +l de 1 en 1.

Finalmente, en la resolución de R(r) aparece de nuevo l y otra constante de separación n que, por un razonamiento análogo al anterior resulta que debe ser mayor o igual a l+1. Deducimos de aquí que el valor más pequeño de n es 1.

Es necesario recordar que estas soluciones no son funciones únicas sino familias de funciones que cumplen los condicionantes de la EdS y que los distintos miembros de las familias vienen dados por los distintos valores permitidos de n, l y m. Y esto es matemáticas, no física.

Bien, pues ya tenemos encontradas las soluciones a la EdS, que tienen la forma general

Ψ = R_nl(r)Θ_lm(θ)Φ_m(φ)

donde, como hemos visto,

n = 1,2,3,...

l = 0,1,2,...,n-1

m = -l, -l+1,...,0,...,l-1,l

Veamos el aspecto de algunas de estas soluciones. Si hacemos n =1, ello implica que l = 0 y m = 0. En este caso Θ(θ) y Φ(φ) se hacen constantes y

Ψ =Ψ(r) = Ae^Br (A,B son constantes de integración)

Para n = 2 tenemos esta misma posibilidad ( l = 0 y m = 0) y tres más a partir de l=1 con m = +1,0,-1, a saber,

Ψ = Ce^Br

Ψ = D r sen θ cos φ e^Br

Ψ = D r sen θ sen φ e^Br

Ψ = D r cos θ e^Br (C, D son constantes de integración)

Y así podríamos seguir para los distintos valores de n, l y m encontrando todos los miembros de la familia de funciones que son solución de la EdS.

Aproximémonos ahora un poco a la terminología física. La representación de las funciones que sólo dependen de r será una esfera, llamemoslas s y distingámolas por el valor de n:

1s = Ae^Br

2s = Ce^Br

Las funciones que tengan l =1, llamémoslas p, distingámolas por su valor de n y marquemos con un subíndice su orientación en ejes cartesianos (transformamos ahora de esféricas a cartesianas):

2p_x = D r sen θ cos φ e^Br = D x e^Br

2p_y = D r sen θ sen φ e^Br = D y e^Br

2p_z = D r cos θ e^Br = D z e^Br

Tenemos de esta forma las funciones de onda reales hidrogenoides para n =1 y n = 2. Un orbital es una función de onda espacial de un electrón. Puesto que en un átomo hidrogenoide solo tiene un electrón, todas sus funciones de onda son orbitales. Éstos tienen la siguiente representación gráfica:

Finalmente damos nombre a nuestras constantes de separación, que llamaremos números cuánticos porque, como hemos visto, adoptan valores discretos (no continuos):

n es el número cuántico principal

l es el númnero cuántico de momento angular y

m es el número cuántico magnético.

Ya podemos comprender la imagen del comienzo de la entrada sabiendo que los números entre paréntesis corresponden a los tres números cuánticos. Y ya está. Lo demás son detalles.