La estructura del azar y el i-Phone 5

Esta entrada tiene dos partes diferenciadas y autocontenidas; si te interesa el aspecto tecnológico exclusivamente puedes pasar a la segunda (Estructura a nanoescala de un vidrio metálico) sin necesidad de leer la primera, de contenido algo más matemático y especulativo.

Proyección ortográfica de un cubo de 5 dimensiones en 2 dimensiones sobrepuesto al patrón de difracción de un cuasicristal icosaédrico

Los servicios de inteligencia sabían muy bien en la época de la Segunda Guerra Mundial la importancia que la verdadera aleatoriedad tenía en los códigos que usaban sus espías para encriptar sus mensajes. Ya habían descubierto durante la Primera, de la forma más dolorosa, que una persona no puede escribir números realmente “al azar” y, por ello, en Bletchly Park, sede de los servicios de contraespionaje británicos, donde trabajó Alan Turing y se descifró el código de la máquina Enigma, había grupos de mujeres arrojando dados con los que construían cuadernos de un solo uso pseudoaleatorios para que los usasen los espías en el continente.

Construir secuencias aleatorias puede parecernos intuitivamente fácil, pero no lo es. No se trata de decir los números (letras o palabras son reducibles a números) que se nos ocurran y y ya está. Hemos de tener cuidado de que no dejemos, inconscientemente, una pauta: tendemos a usar determinadas palabras y estructuras gramaticales, por ejemplo. Pero, paradójicamente, intentar no dejar una pauta, ¡es una pauta! Estos es sólo la manifestación del hecho de que el azar, la pura aleatoriedad, contraintuitivamente, tiene estructura. Veamos un ejemplo.

Intenta escribir una secuencia de números naturales que tú creas que es aleatoria. Una vez que lo hayas hecho estudiala como si la hubiese escrito otra persona y busca pautas; las encontrarás rápidamente. Así, si nos limitamos a los números naturales entre 1 y 15 podríamos haber escrito:

1, 4, 6, 7, 10, 14

que parecen números al azar. Pero a estos números se le puede encontrar una pauta:

a, a+n₁3, b, a+n₂3, a+n₃3, 2(b+1) donde n = 1, 2, 3, ...

Dicho de otra manera, 1,4,7 y 10 forman una progresión aritmética en el que la diferencia entre un término y el siguiente es la misma (3). Sabiendo esto intentemos elegir los números de forma que no haya ningún tipo de pauta apreciable entre ellos:

1, 2, 4,

Con estos números ya no podemos elegir el 6 por que tendríamos 2, 4, 6, así que

1, 2, 4, 5,

y ahora no podemos elegir ni el 7 ni el 8...

Y esto es limitándonos a las progresiones aritméticas. Hemos podido ver que escribir una lista de números al azar no es trivial. De hecho el teorema de Szemerédi prueba que es imposible. Y rizando el rizo, ni siquiera usando números primos te libras del problema, como demuestra el teorema de Green-Tao.

Cuando consideramos los sólidos el concepto de aleatoriedad se asocia a los sólidos amorfos, a los llamados vidrios. En estos se dice que el empaquetamiento de los átomos, la secuencia en la que se colocan es aleatoria. Esto podríamos llegar a la conclusión de que no es cierto gracias a Szemerédi, aunque hay cuestiones puramente químicas que nos hacen intuir que esto no puede ser estrictamente así.

Por su estructura interna los sólidos podemos clasificarlos en cristalinos, cuasicristalinos y amorfos. Como las definiciones estándar de estas estructuras se pueden encontrar fácilmente en la red, nosotros vamos a ir un pasito más allá y hablaremos de hiperdimensiones y de los planteamientos sobre aperiodicidad de Harald Bohr para unificar matemáticamente la visión de las tres. Así, una estructura cristalina sería el corte de una función multidimensional periódica por un hiperplano racional, es decir, la estructura cristalina tridimensional es realmente el corte por un hiperplano según un plano de la celda hexadimensional. Análogamente, en un cuasicristal el corte de la función periódica es irracional (típicamente el número áureo), esto es, el hiperplano que corta no coincide ni puede hacerse coincidir con un plano de la celda hexadimensional.

Vemos que, desde este punto de vista, hemos agotado todas las posibilidades de corte de una celda hexadimensional con los cristales (números racionales) y los cuasicristales (irracionales). Por tanto, podemos conjeturar [lo que no he leído en ningun parte y es original de un servidor] que en un sólido amorfo, de existir hiperestructura, ésta tendrá una dimensionalidad superior a 6 pero finita. Y es finita por el teorema de Szemerédi y porque a corto rango existe orden en todos los sólidos.

Efectivamente, desde el punto de vista del orden tanto cristales como cuasicristales lo tienen a corto a medio y a largo. Es característico de los cuasicristales que existan simetrías icosaédricas, cosa que para los cristales no está permitida, y el orden a largo no es tan evidente. En los vidrios no existe orden a largo (en el sentido habitual del término, hay aleatoriedad), pero sí existe orden a corto porque químicamente los átomos sólo son estables o metaestables en determinados entornos. Se alcanzará un estado estable si la mezcla tiene tiempo y energía como para ordenarse suficientemente, si no, el estado será metaestable. La cuestión es ¿cómo es la transición del orden a corto al desorden a largo? ¿habrá fases cristalinas, cuasicristalinas? ¿Qué ocurre a medio rango?

Un indicio del aspecto que pueden tener las respuestas a estas cuestiones lo proporciona un grupo de investigadores encabezados por Jinwoo Hwang, de la Universidad de Wisconsin en Madison (EE.UU.), con los resultados que han publicado en Physical Review Letters sobre un vidrio metálico.

Estructura a nanoescala de un vidrio metálico.

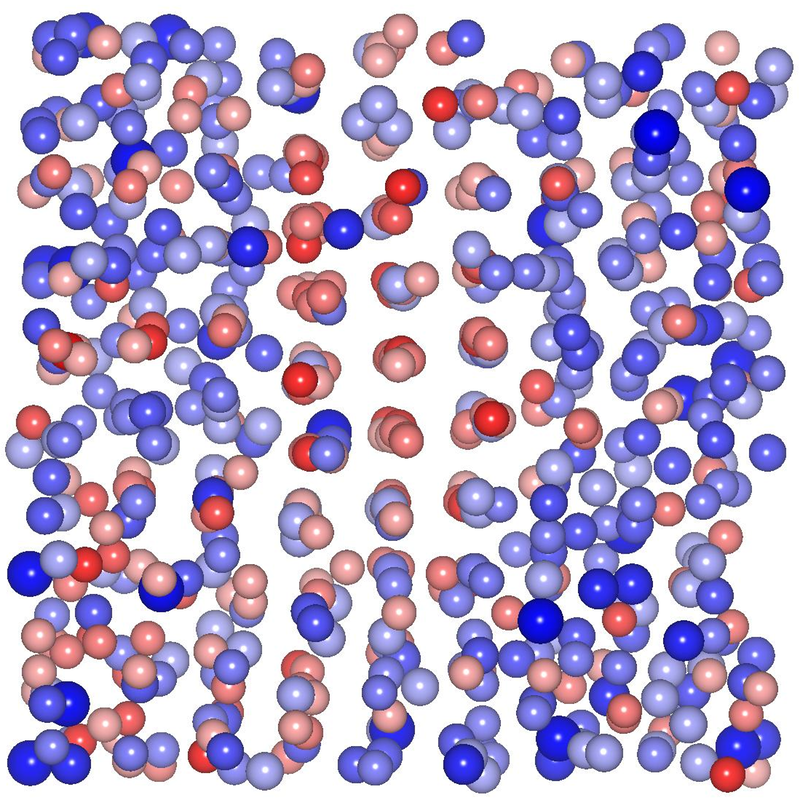Zonas de estructura cúbica (centro) e icosaédrica (bordes) en un vidrio metálico

Los vidrios metálicos (VM) tienen características técnicas muy interesantes: son metales, son fuertes, y resisten muy bien la corrosión y el desgaste. Pero pueden romperse de pronto. El conocimiento que se tiene de su estructura es muy limitado como para poder explicar estas características. El trabajo de Hwang et al., del que damos la referencia más abajo, sugiere que estos materiales contienen más orden de lo que sugiere su nombre.

Los especialistas en materiales sospechan que los VM tienen algún tipo de estructura semiordenada, aún cuando no sea un cristal perfecto. La teoría predominante, apoyada por modelos por ordenador, es que hay “agrupaciones” de átomos, entendiendo por agrupación un átomo central y sus vecinos inmediatos, que forman pentágonos distorsionados o, más bien, icosaedros, sus equivalentes tridimensionales. Estas geometrías tienen simetría traslacional quíntuple, por lo que estaríamos frente a estructuras tipo cuasicristal. Los materiales con esta estructura tienden a quebrarse bajo tensión, en vez de estirarse o doblarse, lo que coincide con los VM. Hay otra teoría que dice que hay varias agrupaciones que se organizan en disposiciones cristalinas de tamaños del orden de un nanometro, pero esto suscita más polémica.

Hwang et al. han añadido datos experimentales a un modelo por ordenador y el resultado es que la realidad sería más compleja que ninguna de estas hipótesis por separado.

El equipo de investigadores usó una técnica llamada microscopía electrónica de fluctuación (FEM, por sus siglas en inglés) para estudiar muestras de un VM de composición Zr₅₀Cu₄₅A_l5. La FEM mide las variaciones en la difracción de los electrones conforme un flujo de éstos se mueve por la superficie de una muestra delgada. Una muestra perfectamente homogénea, ya sea cristalina o amorfa, no tendría variaciones significativas en su modelo de difracción. Pero si la muestra tiene algún tipo de variación en la escala de uno a unos pocos nanometros la difracción cambiará de forma significativa. La técnica, por tanto, es sensible a lo que se denomina rango medio, el rango donde la microscopía electrónica convencional o la difracción rayos X tiene dificultades.

Los datos de la FEM se introdujeron en una simulación por ordenador (Montecarlo híbrida inversa) con el resultado de que diferentes zonas de la muestra tenían diferentes simetrías. Unas eran icosaédricas y otras eran cúbicas. Las zonas cúbicas podían llegar a ser el 15% de la muestra. Como ésta se había enfriado muy rápidamente desde su estado fundido, la estructura alcanzada es muy probable que sea metaestable.

Efectivamente, cuando la muestra se calentaba durante una hora a la temperatura de la habitación, el porcentaje de zona cristalina caía drásticamente pasando a una estructura icosaédrica. Esta estructura sería más estable, por tanto.

Decimos más estable y no la más estable porque puede que el estado alcanzado sea el de energía más baja. Esto, unido a que el estudio se refiere a un VM muy concreto, implica que no se puede generalizar el resultado a otros tipos de VM con facilidad. Pero, como todos los VM se fabrican por enfriamiento muy rápido, sí nos da indicios de lo que puede llegar a ocurrir con su uso industrial.

El iPhone 5 y los vidrios metálicos

Una de las características de los vidrios es que no tienen una temperatura de fusión, es decir, una temperatura a la que pasan del estado sólido al líquido. Por el contrario la transición de sólido a líquido es continua: los vidrios pueden visualizarse como líquidos de viscosidad muy próxima a infinita que, conforme se calientan, van disminuyendo progresivamente, empezando a fluir cada vez más. Esto los asemeja a los plásticos, que se van “derritiendo” cuando los calentamos haciéndose cada vez más maleables.

A diferencia, por tanto, de las aleaciones metálicas habituales, los vidrios metálicos pueden moldearse como el plástico: los puedes aspirar, empujar, soplar o lo que se te ocurra para que adopten formas muy complicadas sin pérdida de material y sin mecanización.

Si esto sigue siendo cierto incluso a micro o nanoescala podrías fabricar haces de nanocables o microengranajes para micromotores. El problema surge con el comportamiento a medio rango, que viene condicionado por la más que posible existencia de estructuras cristalinas metaestables, en principio, no deseadas.

Si el rumor de que el próximo iPhone 5 usará intensivamente VM es cierto, Apple estaría poniendo un montón de fe en un material cuyas características los científicos sólo están empezando a comprender.

Esta entrada es una participación de Experientia docet en la XV Edición del Carnaval de Química que organiza El cuaderno de Calpurnia Tate.

Referencia:

Hwang, J., Melgarejo, Z., Kalay, Y., Kalay, I., Kramer, M., Stone, D., & Voyles, P. (2012). Nanoscale Structure and Structural Relaxation in Zr_{50}Cu_{45}Al_{5} Bulk Metallic Glass Physical Review Letters, 108 (19) DOI: 10.1103/PhysRevLett.108.195505