 |
| Torre Azul de Magarheh (Irán) |
Hace unos meses y con motivo de la concesión del premio Nobel de
química a Daniel Shechtman, hablábamos del arte geométrico
islámico y cómo los patrones de diseño bidimensionales
correspondían a las pautas de los cuasicristales. Esos patrones se
habrían formado por teselación con azulejos, de abajo a arriba.
Ahora Rima al Ajlouni, de la Tech University de Texas (EE.UU.),
afirma haber encontrado ejemplos perfectos de estructuras
cuasiperiódicas en la decoración de tres edificios medievales
islámicos y demuestra que la construcción de los mismos no se
realiza por teselación, apuntando que es necesario tan sólo regla y
compás. Los resultados se publican en Acta Crystallographica
Section A [1].
Desde que se descubriesen los cuasicristales en los años 80 del
siglo XX tanto científicos como especialistas en artes decorativas
se habían dado cuenta de la semejanza entre la decoración de
algunos lugares de culto islámicos y las estructuras geométricas
cuasiperiódicas. Una característica fundamental compartida es que
las pautas son diferentes dependiendo del tamaño de la región
observada.
En 2007 Peter Lu (Harvard) y Paul Steinhardt (Princeton)
informaron [2] en Science de que habían encontrado un ejemplo
de patrón geométrico del siglo XV en Isfahán (Irán) que
representaba una teselación de Penrose casi perfecta. Tal y
como explicamos en Arte islámico y cuasicristales, los
investigadores concluían que los artesanos probablemente hubiesen
creado los patrones usando un conjunto de azulejos de distintas
formas, cada uno decorado con líneas que se unían para formar la
estructura final. Es decir, que el motivo se construía por leyes
locales, con azulejos que se podían dividir y solapar. Ninguno de
los métodos propuestos por distintos investigadores ha conseguido
explicar, sin embargo, como estos artesanos terminaban proporcionando
una armonía general a sus diseños.
 |
| Madraza al Attarin de Fez (Marruecos) |
Al Ajlouni afirma haber encontrado tres ejemplos de patrones
cuasiperiódicos sin imperfecciones en edificios medievales
islámicos. El primer patrón es el conocido como “rueda de carro”
y es característicos de la arquitectura selyúcida (un imperio que
se extendió desde Turquía a Afganistán). Al Ajlouni encuentra
ejemplos en el Santuario de los Imames (Darb-i Imam, 1453),
precisamente el edificio que más estudiaron Lu y Steinhardt, y la
Mezquita del Viernes (también llamada mezquita jameh, o gran
mezquita; alrededor de 1100), ambos en Isfahán. El segundo patrón
aparecería en las paredes interiores del patio de la madraza
al-Attarin (1323) de Fez (Marruecos, 1323). Finalmente, el tercero,
también estudiado por Lu y Steinhardt aparece en la paredes externas
de la Torre Azul (Gunbad-i Kabud, 1197) en Maragheh (Irán).
La autora muestra en el artículo que los antiguos diseñadores
islámicos fueron capaces de resolver los problemas a rangos grandes
que origina la cuasiperiodicidad. En los tres ejemplos considerados,
Ajlouni reconstruye los patrones y muestra que el tamaño de la
figura “semilla” central es proporcional al tamaño del marco
general del patrón. No sólo eso, también demuestra que pueden
construirse empleando tan sólo regla y compás.
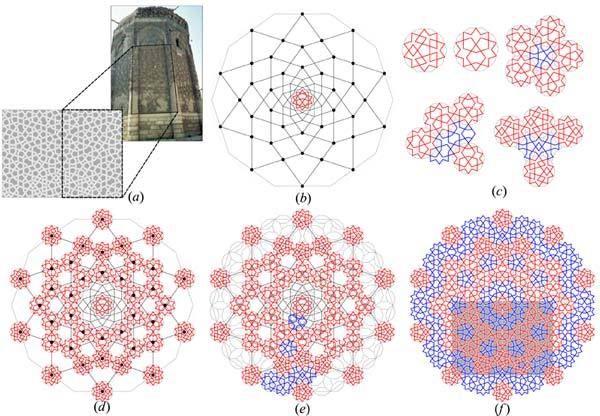 |
| "Semilla" y desarrollo del patrón de la Torre Azul de Magarheh |
Si bien el hallazgo es interesante, lo es más desde el punto de
vista matemático, revelando el nivel alcanzado por los artesanos
islámicos, que químico o de ciencia de los materiales, como
pretende la autora. La estructura de los cuasicristales ya ha sido
determinada con gran precisión, experimental y matemáticamente (la
cuestión candente es cómo crecen de esta manera, pero este es otro
tema).
Referencias:
[1] Al Ajlouni, R. (2012). The global long-range order of quasi-periodic patterns in Islamic architecture Acta Crystallographica Section A Foundations of Crystallography, 68 (2) DOI: 10.1107/S010876731104774X
[2] Lu, P., & Steinhardt, P. (2007). Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture Science, 315 (5815), 1106-1110 DOI: 10.1126/science.1135491
No hay comentarios:
Publicar un comentario